Hey, it’s Zara Dad, and in this Post ” Intuitive Approach to Understanding Probability Post By Zara Dar ” we’re going to be talking about probability. Probability has all sorts of practical applications in a variety of fields, including machine learning. In machine learning, probability is used to model uncertainty, make predictions, and assess the confidence of those predictions. If you’d like me to go into more detail on how probability is used in machine learning, please let me know in the comments.
The purpose of this Post is to give you some intuition on what probability is. By the end of this Post, you will hopefully have an intuitive overview of the subject. I will also be getting into some specifics behind the three probability axioms that govern how to approach solving problems, and I’ll be doing all of this through a very simple example.
So, let’s get started. In the most narrow view, we can say that probability is just a branch of mathematics. We have some fundamental axioms that govern how to solve such problems, and we consider models that satisfy these axioms.
Probability as Frequencies and Sample Space
If you are unfamiliar with what an axiom is, simply put, an axiom is a starting point in mathematics, and it provides us with the basic underlying structure of probability. We can do all of this without ever really asking what the word “probability” really means.
Very, very loosely speaking, we can say that probabilities can be interpreted as frequencies. As an example, let’s start with the description of possible outcomes of a simple experiment. Let’s say I toss a fair coin infinitely many times. It has a certain number of possible outcomes—two, specifically, in this case: heads and tails.
We start by making a list of the possible outcomes, or a better word than the word “list” would be the word “set,” which has a more formal mathematical meaning. So, we create a set that we usually denote by the capital Omega. That set is called a sample space, and it is the set of all possible outcomes of our experiment.
The elements of a set should have certain properties, namely, the elements should be mutually exclusive and collectively exhaustive. So, what does that mean?
Mutually exclusive means that if, at the end of the experiment, I tell you that a certain outcome has happened, then it should not be possible that another outcome has also happened. In the case of this coin flip, you will get either a heads or a tails. It is not possible to have both outcomes, so at the end of the experiment, only one of the outcomes could have happened.
Being collectively exhaustive means something else—that together, all of the elements of the set exhaust all the possibilities. No matter what, at the end, you’ll be able to point to one of the outcomes and say that that one has occurred.
In the sample space depicted here, the two elements of this set, heads and tails, exhaust all possible outcomes. To summarize, this set should be such that, at the end of the experiment, you should always be able to point to one, and exactly one, of the possible outcomes and say that this is the outcome that has happened.
Fundamental Axioms and Real-World Applications
As we repeat this coin flip experiment a large number of times under similar conditions—so as we keep flipping the coin over and over again—it appears that the relative frequency of obtaining heads gets closer and closer to 0.5. Therefore, you may be inclined to say that the probability that we obtain heads is 0.5.
Each event, heads or tails, has a certain non-negative probability assigned to it. This is known as the non-negativity axiom. In our experiment, we have two subsets that make up the entire sample space. The probability of heads and tails together must sum up to one. This is known as the normalization axiom.
We can add these two probabilities—the probability of heads and the probability of tails—because they are two disjoint sets. In mathematics, being disjoint means that their intersection has no elements in it. This can easily be seen in this illustration here. There’s no overlap between the two sets.
In other words, this means that their intersection is the empty set, and this is known as the additivity axiom. Just so you don’t get confused on the notation, this symbol here, which looks like a “U,” means the union of two sets.
As a quick illustration to show you what the union of two sets looks like, we can say that we have sets A and B here. Where they overlap is called the union.
The entirety of probability rests on these three fundamental axioms, from which we can derive other axioms. In a sense, the probability of event A can be interpreted as the frequency with which event A will occur in an infinite number of repetitions of the experiment.
But is that all there is? Are probabilities really frequencies? If we’re dealing with simple coin tosses, it might make sense to think of probabilities as frequencies.
But consider the following statement: “The current president of my country will be reelected in the next election with probability 7.” It’s hard to think of this number 7 as a frequency. It does not make much sense to think of infinitely many repetitions of the next election.
In cases like this, and in many other cases, it is better to think of probabilities as just some way of describing our beliefs. If you’re someone who likes to make bets, then probabilities can be thought of as some numerical guidance into what kind of bets you might be willing to make.
But now, if we think of probabilities as beliefs, you can run into the argument that, well, aren’t beliefs subjective? And isn’t probability theory supposed to be an objective part of math and science? Is probability just an exercise in subjectivity?
Well, not quite. There’s obviously more to it. Probability, at the minimum, gives us some rules for thinking systematically about uncertain situations. If it just happens that our probability model and our subjective beliefs have some relation with the real world, then probability theory can be a very useful tool for making decisions and predictions.
Now, whether your predictions and decisions will be any good will depend on whether you have chosen a good model. Have you chosen a model that provides a good enough representation of the real world?
And how do you make sure that this is the case? Well, lucky for you, there’s a whole field—the field of statistics—whose purpose is to complement probability theory by using data to come up with good models.
So, we have the following diagram that summarizes the relation between the real world, statistics, and probability.
The real world generates data. The field of statistics and inference uses the data to come up with probabilistic models. Once we have a probabilistic model, we can use probability theory and the analysis tools that it provides to us. The results that we get from this analysis lead to predictions and decisions about the real world.
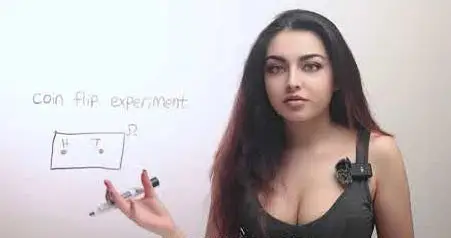
Leave a Reply